準備中

 今回の授業は班ごとの課題研究の発表です。

Googleスライドを作成して、プロジェクタで投影して発表です。

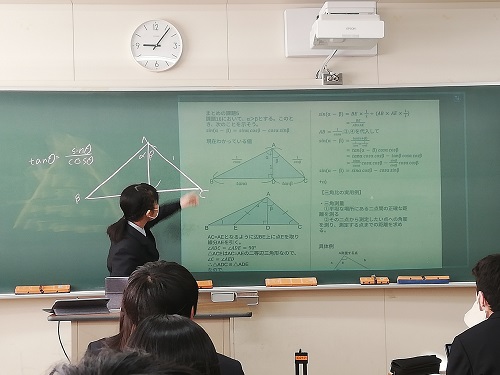
まず教科書に掲載されている課題研究に取り組み、それについてさらに発展的な内容について研究し、各班工夫して発表しました。
 この班は「三角比の値と正弦定理」という課題のもとに発展的な三角関数の公式の証明について取り組みました。
1年生ながら、数学Ⅱの加法定理の証明と、発展的内容である3倍角の公式の証明をしています。
 
 発表後、先生からのコメントがあります。

「sin(θ-90°)=-cosθとcos(θ-90°)=sinθの証明をしてくれるかな？」

「ええと…」

その場でなんとか証明をしようと頑張ります。
  次は「開平法」について取り組んだ班です。
まず教科書の課題の「開平方」の説明から始まり、自分たちで調べた「古代ギリシアの方法」、さらに発展して「N乗根」について検証していきます。どちらも教科書には載っていません。よく調べてきましたね！
 
 スプレッドシートを使って、N乗根を実際に調べています。
Googleのアプリを使いこなしています！
 この班は「立体とそれに内接する球」を課題研究に選びました。

最初は教科書にある「３，４、５の比の長さの直角三角形を底面とする三角柱に内接する球」について調べて、発展して正四面体に接する球について調べました。

実際に立体を作っています。素晴らしい出来です！
 
 この班は「黄金比」を課題に選んで研究です。
黄金比とフィボナッチ数の関係に着目し、フィボナッチ数列の一般項を求めていきます。
 
 これは…2、３年生でも相当難しいぞ！
正確な証明がされました。
 画面が見づらくてすみません。

この班の課題研究は「絶対値を含む関数」です。教科書の問題は絶対値が一つだけですが、発展してｎ個の絶対値を含んだ「y=|x-1|+|x-2|+・・・+|x-n|」のグラフの検証です。

ｎが偶数、奇数で場合分けして、奇数の時は頂点がある、ということを発見。スプレッドシートで頂点の動きを見ています。
 頂点の動きはどうなっているのか…？
発表したこと以上に、今思いついたことも即席で発表してくれました。画面がちゃんと見えませんが、頂点の動きは放物線を描いています。

発展的な内容を研究する班が多く、見ごたえのある発表でした。みんな集中して他の班の発表を聞いていました。

数学への理解、興味が深まったのではないでしょうか。